Eksponentni integral

Grafa funkcij E₁ (zgoraj) in Ei (spodaj)

Eksponéntni integrál (tudi integrálna eksponéntna fúnkcija, označba Ei) je v matematiki specialna nelementarna funkcija v kompleksni ravnini. Definirana je kot poseben določeni integral razmerja med eksponentno funkcijo in njegovim argumentom.

Definicije

Za realne neničelne vrednosti x je eksponentni integral Ei(x) definiran kot:

$\operatorname {Ei} (x)=-\int _{-x}^{\infty }{\frac {e^{-t}}{t}}\,\mathrm {d} t\!\,.$

Rischev algoritem pokaže, da funkcija Ei ni elementarna. Zgornja definicija se lahko uporabi za pozitivne vrednosti x, vendar je treba integral razumeti v smislu Cauchyjeve glavne vrednosti zaradi singularnosti integranda v točki 0.

Za kompleksne vrednosti argumenta je ta definicija dvoumna zaradi vejišč v 0 in $\infty$. Zaradi tega se namesto Ei uporablja naslednji zapis:

$\mathrm {E} _{1}(z)=\int _{z}^{\infty }{\frac {e^{-t}}{t}}\,\mathrm {d} t,\qquad (|{\rm {Arg}}(z)|<\pi )\!\,.$

V splošnem je prerez vejišča vzet na negativni realni osi in se lahko funkcija E₁ definira z analitičnim nadaljevanjem vseepovsod drugod v kompleksni ravnini.

Za pozitivne vrednosti realnega dela $z$ se lahko to zapiše kot:

$\mathrm {E} _{1}(z)=\int _{1}^{\infty }{\frac {e^{-tz}}{t}}\,\mathrm {d} t=\int _{0}^{1}{\frac {e^{-z/u}}{u}}\,\mathrm {d} u,\qquad (\Re (z)\geq 0)\!\,.$

Obnašanje funkcije E₁ blizu prereza vejišča se lahko vidi z naslednjim izrazom:

$\lim _{\delta \to 0+}\mathrm {E_{1}} (-x\pm i\delta )=-\mathrm {Ei} (x)\mp i\pi ,\qquad (x>0)\!\,.$

Značilnosti

Več spodnjih značilnosti eksponentnega integrala v določenih primerih omogoča izogib eksplicitni določitvi vrednosti prek zgornje definicije.

Konvergentne vrste

Če se integrira Taylorjeva vrsta za $e^{-t}/t\,$ in izloči logoritemska singularnost, se lahko izpelje naslednji razvoj v vrsto za funkcijo $\mathrm {E} _{1}(x)\,$ za realne $x\,$:

$\operatorname {Ei} (x)=\gamma +\ln |x|+\sum _{k=1}^{\infty }{\frac {x^{k}}{k\;k!}},\qquad (x\neq 0)\!\,.$

Za kompleksne argumente stran od negativne realne osi se to posploši v:

$\mathrm {E} _{1}(z)=-\gamma -\ln z-\sum _{k=1}^{\infty }{\frac {(-z)^{k}}{k\;k!}},\qquad (|\mathrm {Arg} (z)|<\pi )\!\,,$

kjer je $\gamma \,$ Euler-Mascheronijeva konstanta. Vsota konvergira za vse kompleksne $z$, tako da se za običajno vrenost kompleksnega logaritma vzame prerez vejišča vzdolž negativne realne osi.

S to formulo se lahko izračuna $\mathrm {E} _{1}(x)\,$ z operacijami s plavajočo vejico za realne $x\,$ med 0 in 2,5. Za $x>2,5\,$ je rezultat netočen zaradi izgube pomembnosti.

Hitreje konvergirajočo vrsto je našel Ramanudžan:

$\operatorname {Ei} (x)=\gamma +\ln x+e^{x/2}\sum _{n=1}^{\infty }{\frac {(-1)^{n-1}x^{n}}{n!\,2^{n-1}}}\sum _{k=0}^{\lfloor (n-1)/2\rfloor }{\frac {1}{2k+1}}\!\,.$

Asimptotične (divergentne) vrste

Relativna napaka asimptotičnega približka za različno število členov $~N~$ v prisekani vsoti

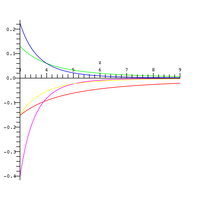
Konvergenca zgornje vrste je počasna za argumente z večjim modulom. Za $x=10\,$ je na primer potrebno več kot 40 členov za vrednost točno na tri decimalna mesta. Obstaja pa približek z divergentno vrsto, ki se lahko dobi z integracijo $ze^{z}\mathrm {E} _{1}(z)\,$ po delih:

$\mathrm {E} _{1}(z)={\frac {e^{-z}}{z}}\sum _{n=0}^{N-1}{\frac {n!}{(-z)^{n}}}\!\,,$

z napako reda $O(N!z^{-N})\,$ in velja za velike vrednosti $\mathrm {Re} (z)\,$. Relativna napaka zgornjega približka je prikazana na desni sliki za različne vrednosti členov $N\,$ v prisekani vsoti ($N=1\,$ rdeče, $N=5\,$ rožnato).

Eksponentno in logaritemsko obnašanje: izenačevanje

Izenačevanje funkcije $\mathrm {E} _{1}\,$ z dvema elementarnima funkcijama

Iz dveh vrst predlaganih v predhodnih razdelkih sledi, da se funkcija $\mathrm {E} _{1}\,$ obnaša kot negativna eksponentna funkcija za velike vrednosti argumenta in kot logaritem za majhne vrednosti. Za pozitivne realne vrednosti argumenta se lahko funkcija $\mathrm {E} _{1}\,$ izenači z elementarnimi funkcijami kot sledi:

${\frac {1}{2}}e^{-x}\,\ln \!\left(1+{\frac {2}{x}}\right)<\mathrm {E} _{1}(x)<e^{-x}\,\ln \!\left(1+{\frac {1}{x}}\right),\qquad (x>0)\!\,.$

Leva stran te neenakosti je prikazana na levem grafu modro; osrednji del $\mathrm {E} _{1}(x)\,$ črno, desna stran pa rdeče.

Definicija s funkcijo Ein

Obe funkciji $\operatorname {Ei} \,$ in $\mathrm {E} _{1}\,$ se lahko zapišeta preprostejši obliki s pomočjo cele funkcije $\operatorname {Ein} \,$, definirane kot:

$\operatorname {Ein} (z)=\int _{0}^{z}(1-e^{-t}){\frac {\mathrm {d} t}{t}}=\sum _{k=1}^{\infty }{\frac {(-1)^{k+1}z^{k}}{k\;k!}}\!\,.$

(to je le alternirajoča vrsta v zgornji definiciji funkcije $\mathrm {E} _{1}\,$). Potem velja:

$\mathrm {E} _{1}(z)\,=\,-\gamma -\ln z+\operatorname {Ein} (z),\qquad (|\mathrm {Arg} (z)|<\pi )\!\,.$

$\operatorname {Ei} (x)\,=\,\gamma +\ln x-\operatorname {Ein} (-x),\qquad (x>0)\!\,.$

Povezava z drugimi funkcijami

EKsponentni integral je v tesni povezavi z logaritemskim integralom li(x) s formulo:

$\operatorname {li} (x)=\operatorname {Ei} (\ln x)\!\,,$

za pozitivne realne vrednosti $x\,$.

Eksponentni integral se lahko posploši na:

$\operatorname {E} _{n}(x)=\int _{1}^{\infty }{\frac {e^{-xt}}{t^{n}}}\,\mathrm {d} t\!\,,$

kar se lahko zapiše kot poseben primer nepopolne funkcije gama:

$\operatorname {E} _{n}(x)=x^{n-1}\Gamma (1-n,x)\!\,.$

Posplošena oblika se včasih imenuje Misrova funkcija, $\varphi _{m}(x)\,$, definirana kot:

$\varphi _{m}(x)=\operatorname {E} _{-m}(x)\!\,.$

Z upoštevanjem logaritma se definira posplošena integralsko-eksponentna funkcija:

$\operatorname {E} _{s}^{j}(z)={\frac {1}{\Gamma (j+1)}}\int _{1}^{\infty }(\log t)^{j}{\frac {e^{-zt}}{t^{s}}}\,\mathrm {d} t\!\,.$

Nedoločeni integral:

$\operatorname {Ei} (a\cdot b)=\iint e^{ab}\,\mathrm {d} a\,\mathrm {d} b\!\,$

je po obliki podoben navadni rodovni funkciji za $d(n)\,$, številu deliteljev $n\,$:

$\sum \limits _{n=1}^{\infty }d(n)x^{n}=\sum \limits _{a=1}^{\infty }\sum \limits _{b=1}^{\infty }x^{ab}\!\,.$

Odvajanje

Odvode posplošenih funkcij $\operatorname {E} _{n}\,$ se lahko izračuna s formulo:

$\operatorname {E} _{n}'(z)=-\operatorname {E} _{n-1}(z),\qquad (n=1,2,3,\ldots )\!\,.$

Funkcija $\operatorname {E} _{0}\,$ se preprosto izračuna, zaradi česar je ta rekurzija uporabna, ker velja $e^{-z}/z\,$.

Eksponentni integral imaginarnega argumenta

Graf funkcije $\operatorname {E} _{1}(ix)\,$ v odvisnosti od $x\,$; realni del črno, imaginarni del rdeče.

Če je $z\,$ imaginaren, ima nenegativni realni del, tako da se lahko uporabi formula:

$\operatorname {E} _{1}(z)=\int _{1}^{\infty }{\frac {e^{-tz}}{t}}dt\!\,$

za povezavo s trigonometričnima integraloma $\operatorname {Si} \,$ in $\operatorname {Ci} \,$:

$\operatorname {E} _{1}(ix)=i\left(-{\tfrac {1}{2}}\pi +\operatorname {Si} (x)\right)-\operatorname {Ci} (x),\qquad (x>0)\!\,.$

Realna in imaginarna dela funkcije $\operatorname {E} _{1}(x)\,$ sta prikazana na desni sliki s črno in rdečo krivuljo.

Računanje in približki

Za funkcijo eksponentnega integrala obstaja več približkov. Med njimi so:

• približek Swameeja in Ohije:

${\mathsf {E}}_{1}[x]=(A^{-7.7}+B)^{-0.13}\!\,,$

kjer je $A=\ln {\bigg [}{\bigg (}{\frac {0,56146}{x}}+0,65{\bigg )}(1+x){\bigg ]}$ in $B=x^{4}e^{7,7x}(2+x)^{3,7}\,$,

• približek Allena in Hastingsa:

${\mathsf {E}}_{1}[x]={\begin{cases}\ln {x}+{\textbf {a}}^{T}{\textbf {x}}_{5},&x\leq 1\\{\frac {e^{-x}}{x}}{\frac {{\textbf {b}}^{T}{\textbf {x}}_{4}}{{\textbf {c}}^{T}{\textbf {x}}_{4}}},&x\geq 1\end{cases}}$

kjer je ${\textbf {a}}\triangleq [-0,57722,0,99999,-0,24991,0,5519,-0,00976,0,00108]^{T}\,$, ${\textbf {b}}\triangleq [0,26777,8,63476,18,05902,8,57333]^{T}\,$, ${\textbf {c}}\triangleq [3,95850,21,09965,25,63296,9,57332]^{T}\,$ in ${\textbf {x}}_{k}\triangleq [x^{0},x^{1},\dots ,x^{k}]^{T}\,$,

• razvoj z verižnim ulomkom:

${\mathsf {E}}_{1}[x]={\cfrac {e^{-x}}{x+{\cfrac {1}{1+{\cfrac {1}{x+{\cfrac {2}{1+{\cfrac {2}{x+{\cfrac {3}{\dots }}}}}}}}}}}}\!\,,$

• približek Barryja s sodelavcema:

${\mathsf {E}}_{1}[x]={\frac {e^{-x}}{G+(1-G)e^{-x/(1-G)}}}\ln {\bigg [}1+{\frac {G}{x}}-{\frac {1-G}{(h+bx)^{2}}}{\bigg ]}\!\,,$

kjer je $h={\frac {1}{1+x{\sqrt {x}}}}+{\frac {h_{\infty }q}{1+q}}\,$, $q={\frac {20}{47}}x^{\sqrt {31/26}}\,$, $h_{\infty }={\frac {(1-G)(G^{2}-6G+12)}{3G(2-G)^{2}b}}\,$, $b={\sqrt {\frac {2(1-G)}{G(2-G)}}}\,$, $G=e^{-\gamma }\,$, in tu $\gamma \,$ Euler-Mascheronijeva konstanta.

Posebne vrednosti

$\operatorname {Ei} (0)=-\infty \!\,,$

$\operatorname {Ei} (1/5)=-0,821760587902400315653310869899\ldots \!\,,$

$\operatorname {Ei} (1/4)=-0,542543264661913729533531851734\ldots \!\,,$

$\operatorname {Ei} (1/3)=-0,158092108971155710313577306230\ldots \!\,,$

$\operatorname {Ei} (1/2)=0,454219904863173579920523812662\ldots \!\,,$

$\operatorname {Ei} (1)=1,895117816355936755466520934331\ldots \!\,,$ (OEIS A091725),

$\operatorname {Ei} (2)=4,954234356001890163379505130227\ldots \!\,,$

Ničla ($\operatorname {Ei} (x)=0\,$) ima vrednost:

$x=0,372507410781366634461991866580\ldots \!\,,$ (OEIS A091723).

Uporaba

• časovno odvisni prenos toplote
• neravnovesni tok podtalnice v prehodni Theisovi rešitvi (funkcija vodnjaka)
• prenos sevanja v zvezdnih atmosferah
• radialna difuzijska enačba za tok prehodnega ali spremenljivega stanja s črtastimi viri in ponori
• rešitve nevtronske transportne enačbe v poenostavljenih enorazsežnih geometrijah.

Glej tudi

• Goodwin-Statonov integral

Viri

• Abramowitz, Milton; Stegun, Irene Anne (1964), Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, Abramowitz and Stegun, New York: Dover, ISBN 0-486-61272-4, Poglavje 5
• Barry, D. A.; Parlange, J. -Y.; Li, L. (31. januar 2000), »Approximation for the exponential integral (Theis well function)«, Journal of Hydrology, 227 (1–4): 287–291, Bibcode:2000JHyd..227..287B, doi:10.1016/S0022-1694(99)00184-5
• Bell, George I.; Glasstone, Samuel (1970), Nuclear Reactor Theory, Van Nostrand Reinhold Company
• Bender, Carl M.; Orszag, Steven A (1978), Advanced mathematical methods for scientists and engineers, McGraw–Hill, ISBN 0-07-004452-X
• Bleistein, Norman; Handelsman, Richard A. (1986), Asymptotic Expansions of Integrals, Dover, ISBN 0-486-65082-0
• Busbridge, Ida W. (1950), »On the integro-exponential function and the evaluation of some integrals involving it«, Quart. J. Math. (Oxford), 1 (1): 176–184, Bibcode:1950QJMat...1..176B, doi:10.1093/qmath/1.1.176
• Chiccoli, C.; Lorenzutta, S.; Maino, G. (1988), »On the evaluation of generalized exponential integrals E_ν(x)«, J. Comput. Phys., 78: 278–287, Bibcode:1988JCoPh..78..278C, doi:10.1016/0021-9991(88)90050-2
• Chiccoli, C.; Lorenzutta, S.; Maino, G. (1990), »Recent results for generalized exponential integrals«, Computer Math. Applic., 19 (5): 21–29, doi:10.1016/0898-1221(90)90098-5
• Giao, Pham Huy (1. maj 2003), »Revisit of Well Function Approximation and An Easy Graphical Curve Matching Technique for Theis' Solution«, Ground Water, 41 (3): 387–390, doi:10.1111/j.1745-6584.2003.tb02608.x, ISSN 1745-6584
• Kölbig, K. S. (1983), »On the integral exp(−μt)t^ν−1log^mt dt«, Math. Comput, 41 (163): 171–182, doi:10.1090/S0025-5718-1983-0701632-1
• MacLeod, Allan J. (2002), »The efficient computation of some generalised exponential integrals«, J. Comput. Appl. Math., 148 (2): 363–374, Bibcode:2002JCoAm.138..363M, doi:10.1016/S0377-0427(02)00556-3
• Milgram, M. S. (1985), »The generalized integro-exponential function«, Mathematics of Computation, 44 (170): 443–458, doi:10.1090/S0025-5718-1985-0777276-4, JSTOR 2007964, MR 0777276
• Misra, Rama Dhar; Born, Max (1940), »On the Stability of Crystal Lattices. II«, Mathematical Proceedings of the Cambridge Philosophical Society, 36 (2): 173, Bibcode:1940PCPS...36..173M, doi:10.1017/S030500410001714X
• Press, William Henry; Teukolsky, Saul Arno; Vetterling, William T.; Flannery, Brian P. (2007), »Section 6.3. Exponential Integrals«, Numerical Recipes: The Art of Scientific Computing (3. izd.), New York: Cambridge University Press, ISBN 978-0-521-88068-8, arhivirano iz prvotnega spletišča dne 11. avgusta 2011, pridobljeno 21. januarja 2016
• Sharma, R. R.; Zohuri, Bahman (1977), »A general method for an accurate evaluation of exponential integrals E₁(x), x>0«, J. Comput. Phys., 25 (2): 199–204, Bibcode:1977JCoPh..25..199S, doi:10.1016/0021-9991(77)90022-5
• Stankiewicz, A. (1968), »Tables of the integro-exponential functions«, Acta Astronomica, 18: 289, Bibcode:1968AcA....18..289S
• Stöcker, Horst (2006), Matematični priročnik z osnovami računalništva, Ljubljana: Tehniška založba Slovenije, COBISS 229576192, ISBN 86-365-0587-9
• Temme, N. M. (2010), »Exponential, Logarithmic, Sine, and Cosine Integrals«, v Olver, Frank William John; Lozier, Daniel M.; Boisvert, Ronald F.; Clark, Charles W. (ur.), NIST Handbook of Mathematical Functions, Cambridge University Press, ISBN 978-0521192255,
• Tseng, Peng-Hsiang; Lee, Tien-Chang (26. februar 1998), »Numerical evaluation of exponential integral: Theis well function approximation«, Journal of Hydrology, 205 (1–2): 38–51, Bibcode:1998JHyd..205...38T, doi:10.1016/S0022-1694(97)00134-0

Zunanje povezave

• Hazewinkel, Michiel, ur. (2001), »Integral exponential function«, Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4 (angleško)
• NIST documentation on the Generalized Exponential Integral (angleško)
• Weisstein, Eric Wolfgang. »Exponential Integral«. MathWorld.
• Weisstein, Eric Wolfgang. »En-Function«. MathWorld.
• Exponential integral Ei na strani Wolfram Functions (angleško)
• Eksponentni, logaritemski, sinusni in kosinusni integral v DLMF (angleško)